Los conjuntos son colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.
Los razonamientos y técnicas de la teoría de conjuntos se apoyan en gran medida en la lógica matemática.
El desarrollo histórico de la teoría de conjuntos se atribuye a Georg Cantor, que comenzó a investigar cuestiones conjuntistas "puras" en la segunda mitad del siglo XIX.
Dados unos elementos, unos objetos matemáticos —como números o polígonos por ejemplo—, puede imaginarse una colección determinada de estos objetos, un conjunto.
Los razonamientos y técnicas de la teoría de conjuntos se apoyan en gran medida en la lógica matemática.
El desarrollo histórico de la teoría de conjuntos se atribuye a Georg Cantor, que comenzó a investigar cuestiones conjuntistas "puras" en la segunda mitad del siglo XIX.
Dados unos elementos, unos objetos matemáticos —como números o polígonos por ejemplo—, puede imaginarse una colección determinada de estos objetos, un conjunto.
Cada uno de estos elementos pertenece al conjunto, y esta noción de pertenencia es la relación relativa a conjuntos más básica.
Los propios conjuntos pueden imaginarse a su vez como elementos de otros conjuntos. La pertenencia de un elemento a a un conjunto A se indica como a ∈ A.
Una relación entre conjuntos derivada de la relación de pertenencia es la relación de inclusión.
Una relación entre conjuntos derivada de la relación de pertenencia es la relación de inclusión.
Una subcolección de elementos B de un conjunto dado A es un subconjunto de A, y se indica como B ⊆ A.
Los conjuntos numéricos usuales en matemáticas son: el conjunto de los números naturales N, el de los números enteros Z, el de los números racionales Q, el de los números reales R y el de los números complejos C.
Cada uno es subconjunto del siguiente:
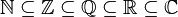
Existen unas operaciones básicas que permiten manipular los conjuntos y sus elementos, similares a las operaciones aritméticas, constituyendo el álgebra de conjuntos:
Unión. La unión de dos conjuntos A y B es el conjunto A ∪ B que contiene cada elemento que está por lo menos en uno de ellos.
Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B.
Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.
Complemento. El complemento de un conjunto A es el conjunto A∁ que contiene todos los elementos (respecto de algún conjunto referencial) que no pertenecen a A.
Diferencia simétrica La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer elemento a pertenece a A y su segundo elemento b pertenece a B.
Cantor partió de la convicción platonista de que era posible “comprimir” una colección o conjunto de objetos y considerarla como un todo (o mejor dicho, como una sola entidad), y al parecer, aceptando implícitamente los supuestos siguientes:
(i) Un conjunto es una reunión de objetos que cumplen con cierta propiedad (llamados los elementos de ese conjunto) y que, por tanto, queda definido por tal propiedad.
(ii) Un conjunto es una sola entidad matemática, de modo que puede a su vez ser contenido por otro conjunto.
(iii) Dos conjuntos que tengan los mismos elementos son iguales. Así, puede decirse que un conjunto está determinado por sus elementos.
El concepto de conjunto se encuentra a un nivel tan elemental que no es posible dar una definición precisa del mismo. Palabras como colección, reunión, agrupación, y algunas otras de significado similar, se usan en un intento de describir a los conjuntos, pero no pueden constituir una definición, pues son simplemente un reemplazo de la palabra conjunto. Con todo, en la teoría intuitiva de conjuntos lo anterior es admisible, y se acepta la existencia de un universo o dominio de objetos a partir del cual se construyen los conjuntos, así como también permite tratar conjuntos como una entidad singular. No es de importancia la naturaleza de los objetos, sino el comportamiento de un conjunto como entidad matemática.
De lo dicho anteriormente, parece natural introducir una relación diádica de pertenencia. El símbolo usual para representar esta relación es el símbolo
 , una versión de la letra griega
, una versión de la letra griega  (épsilon). Los segundos argumentos de la relación
(épsilon). Los segundos argumentos de la relación  son llamados conjuntos, y los primeros argumentos son llamados elementos.
son llamados conjuntos, y los primeros argumentos son llamados elementos.Así, si la fórmula  se cumple, se dice que
se cumple, se dice que  es un elemento del conjunto
es un elemento del conjunto  . Si aceptamos que todo es un conjunto, entonces los primeros y segundos argumentos de
. Si aceptamos que todo es un conjunto, entonces los primeros y segundos argumentos de  pertenecen al mismo dominio.
pertenecen al mismo dominio.
La negación de se escribe
se escribe  .
.
 se cumple, se dice que
se cumple, se dice que  es un elemento del conjunto
es un elemento del conjunto  . Si aceptamos que todo es un conjunto, entonces los primeros y segundos argumentos de
. Si aceptamos que todo es un conjunto, entonces los primeros y segundos argumentos de  pertenecen al mismo dominio.
pertenecen al mismo dominio.La negación de
 se escribe
se escribe  .
.Algo más sobre conjuntos:
Se puede definir un conjunto:
-por extensión, enumerando todos y cada uno de sus elementos.
-por comprensión, diciendo cuál es la propiedad que los caracteriza.
Se puede definir un conjunto:
-por extensión, enumerando todos y cada uno de sus elementos.
-por comprensión, diciendo cuál es la propiedad que los caracteriza.
Un conjunto se suele denotar encerrando entre llaves a sus elementos, si se define por extensión,
o su propiedad característica, si se define por comprensión. Por ejemplo:
o su propiedad característica, si se define por comprensión. Por ejemplo:
A := {1,2,3, ... ,n}
B := {pÎ Z | p es par}
B := {pÎ Z | p es par}
Se dice que A está contenido en B (también que A es un subconjunto de B o que A es una parte de B),
y se denota A Í B, si todo elemento de A lo es también de B, es decir, a Î A Þ a Î B.
Dos conjuntos A y B se dicen iguales, y se denota A = B, si simultáneamente A Í B y B Í A;
esto equivale a decir que tienen los mismos elementos (o también la misma propiedad característica).
El conjunto formado por todos los subconjuntos de uno dado A se llama partes de A, y se denota à (A).
Entonces, la relación B Í A es equivalente a decir B Î Ã (A).
y se denota A Í B, si todo elemento de A lo es también de B, es decir, a Î A Þ a Î B.
Dos conjuntos A y B se dicen iguales, y se denota A = B, si simultáneamente A Í B y B Í A;
esto equivale a decir que tienen los mismos elementos (o también la misma propiedad característica).
El conjunto formado por todos los subconjuntos de uno dado A se llama partes de A, y se denota à (A).
Entonces, la relación B Í A es equivalente a decir B Î Ã (A).
Ejemplos:
Si A = {a,b} entonces à (A) = {Æ ,{a},{b},A}.
Si a Î A entonces {a} ÎÃ (A).
Cuando en determinado contexto se consideran siempre conjuntos que son partes de uno dado U,
se suele considerar a dicho U como conjunto universal o de referencia.
Si A = {a,b} entonces à (A) = {Æ ,{a},{b},A}.
Si a Î A entonces {a} ÎÃ (A).
Cuando en determinado contexto se consideran siempre conjuntos que son partes de uno dado U,
se suele considerar a dicho U como conjunto universal o de referencia.
Fuentes consultadas: diversas en internet.
---


No hay comentarios.:
Publicar un comentario